At Poez Inc. we had to upgrade our projects from 32bit to 64bit in memory address width to run on some Operating Systems and be as future proof as possible. As expected this did not go as smooth….

Evolving 32->64

We had just switched on 64-bit in our project in order to comply with an OS’s policy change for its devices. This means that all our variable types who were 32bits wide are now 64bit wide. This is done to allow access for bigger memory spaces, opening up essential 2^64 bytes of byte addressable memory.

Mind you, this product consisted of a game engine which entails all the usual suspects: physics, AI, graphics, audio and other helper libraries for resource management.

After a few expected type changes and expansions, all our “integer” types that required higher precision were upgraded to “long” types. All well and good until we started exercising code that was heavily reliant on bit shifting.

To note that we started pushing the usage of platform independent variables and enforcing that in the code base ( for exampe, the C99 <inttypes.h> header, is one dependency we added).

From our noticeable snags:

Interleaved Data

The first bug came from our image loading sub-module which was doing some interesting bit shifting. This was a relatively easily fixed by changing some types from 32 to 64bit.  Due to how a lot of image formats are tightly packed and also store image data in an interleaved manner it was crucial to set the right offsets both pre and post buffering of data to the graphics card.

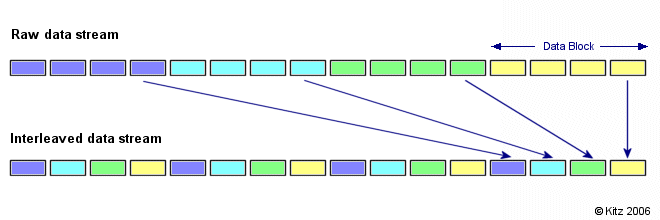
Due to the natural increase in memory usage, we decided to optimize that by keeping track of image memory and just shifting the data back n-bytes (usually was around ~32bits) for every entry in that interleaved array.

We later stripped out all “extended types” and just put those in the beginning of the array and tightly packed the rest in a contiguous manner.

---

Time in 64bit World

On the easier side of the spectrum, naive functions and their return types gave us mini-headaches. The product was highly dependent on high granular time functions.

struct Vertex {
#ifdef __LP64__
    long time_base;
#else
    unsigned int time_base;
#endif

    struct timeval t;

	gettimeofday( &t, NULL );

    time_base = ( ( ( ( t.tv_sec * 1000000 ) + // use 1000000.0 for 64bit
                                       t.tv_usec ) - pz->i_time) * 0.001 );

	return time_base;
}

The function gettimeofday fills the struct…

 

typedef long	__darwin_time_t;	/* time() */
typedef __int32_t	        __darwin_suseconds_t;	/* [???] microseconds */

#define _STRUCT_TIMEVAL		struct timeval
_STRUCT_TIMEVAL
{
	__darwin_time_t	        tv_sec;	        /* seconds */
	__darwin_suseconds_t    tv_usec;        /* and microseconds */
};

..timeval, which contains the variable tv_sec  of type “long” which actually is “long int”. In the 32bit world this was 4 bytes (32bits) but in the 64bit world it increases to 8 bytes (64bits).  This transition’s first issue was the downcasting and loss of precision from “long” to “int”. We changed the function to “unsigned int” to allow for higher range and also since time is always positive.

The loss of precision on time impacted three important modules: Security, Animation and Physics.

Security

Due to the nature of the topic i’ll try to be as vague yet specific. Our security module is heavily reliant on time as it uses a custom system which is akin to evolution in that all our external files and critical resources irreversibly “evolve”. In order to track such growth, we need very precise times in order to generate encryption/decryption keys. Figuring out said time involves bit shifting on the lower end of the container, which is where the loss of precision happens.

Animation

The animation system does some clever interpolations that make up for rendering and update delays. Detecting and predicting delays too involves bit shifting and bit checking in the low bits. This became challenging when going from one animation to another and calculating the appropriate interpolations.

Physics

Akin to Animation, the physics updates too had custom functions which would anticipate delays and make up for that. Scenarios where ray-testing was happening were impacted. This was fixed in a similar manner to animation although some logarithmic functions needed some approximations in order to fix and make up for the errors that stemmed from mis-timings.

---

 

Bullet SDK’s Square Root Function

Our engine is heavily reliant on the physics engine BulletSDK. During the transition we hit a very well hidden bug related to finding the square root of a number.

SIMD_FORCE_INLINE btScalar btSqrt(btScalar y) 
{ 
#ifdef USE_APPROXIMATION
#ifdef __LP64__
    float xhalf = 0.5f*y;
    int i = *(int*)&y;
    i = 0x5f375a86 - (i>>1);
    y = *(float*)&i;
    y = y*(1.5f - xhalf*y*y);
    y = y*(1.5f - xhalf*y*y);
    y = y*(1.5f - xhalf*y*y);
    y=1/y;
    return y;
#else
    double x, z, tempf;
    unsigned long *tfptr = ((unsigned long *)&tempf) + 1;
    tempf = y;
    *tfptr = (0xbfcdd90a - *tfptr)>>1; /* estimate of 1/sqrt(y) */
    x =  tempf;
    z =  y*btScalar(0.5);
    x = (btScalar(1.5)*x)-(x*x)*(x*z);         /* iteration formula     */
    x = (btScalar(1.5)*x)-(x*x)*(x*z);
    x = (btScalar(1.5)*x)-(x*x)*(x*z);
    x = (btScalar(1.5)*x)-(x*x)*(x*z);
    x = (btScalar(1.5)*x)-(x*x)*(x*z);
    return x*y;
#endif
#else
	return sqrtf(y); 
#endif
}

In the second section of the code, namely non __LP64__ part,  there is an interesting bit shifting technique being  done in order to estimate the inverse square root.  Without getting too technical the casting and shifting goes like this:

1. Alias the argument x to an integer, as a way to compute an approximation of log₂(x)
2. use this approximation to compute an approximation of log₂(1/√x)
3. alias back to a float, as a way to compute an approximation of the base-2 exponential
4. refine the approximation using a single iteration of the Newton’s method. (Source)

The 64bit compatible version of the approximation added to the code base uses a better approximation, namely from 0xbfcdd90a to 0x5f375a86. This benefited the shifting as well as Newton’s approximation, requiring less iterations!

The change was accepted (Change #317) by the BulletSDK team making the excellent physics engine compatible with newer platforms!

---

Take Aways

Using platform independent types is crucial and a lot has been already written on the topic. This still doesn’t solve the bit shifting. A lot of bit magic code tends to work on hard assumptions, namely the size of the variables. I’m proposing a helper class which would track size of variables and offset correct shiftings in a flexible manner.

This would go something like this:

    int i = *(int*)&y;
    i = 0x5f375a86 - (i >> 1);

To this:

    BitS i( *(int*)&y );
    i = 0x5f375a86 - ( i >> 1 );

Class BitS would keep track of type size, which can be implied or passed through constructor. The “>>” and “=” functions are overloaded and managed by the class. This class would avoid such issues we hit in our transition from 32 to 64bit and should stand the test time as we move forward to bigger memory address spaces, bandwidths and sizes.