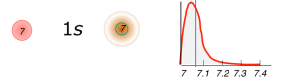
Note: This is not trying to mimic all quantum behaviors although it can be extended to it. This post is to appreciate and analyze benefits of expanding on discrete numbers and entertain systems that run purely in intervals/volumes/clouds(not the servers! 0.0) and continuity.

Yes, we are all waiting for quantum computers to usher in the new era of technology. Heck, If I had the resources, I’d be at the forefront of it. Yet it does not stop us from implementing the new paradigms in our current creations! The main realization in the quantum world is instead of thinking of things as being discrete, in that they can be broken down in to units [1, 2, 3, 4…] it in fact is a very continuous reality as in [1.0, 1.1, 1.2, 1.3…] (see atomic orbital / probability cloud )

s-orbital (max two electrons with angular momentum quantum number ℓ =0)

Notice, it’s a cloud as in an interval rather than a unitary entity.

So how does this translate to programming in binary machines. We’re used to using variables discretely for the most part as in:

    int x = 7;

What I’m proposing simply is defining a type that represents an interval rather than one number:

    QuantumOrb<int> x(7);

Notice the new introduced “QuantumOrb” type and let’s dig in!

   template <class T>
   class Quantum {
       T value;     // Value in Newtonian world.

       // Quantum representation.
       HIGH_PRECISION_TYPE n,   // Principal number (excitedness of quantum cloud
                           l,   // Angular Momentum (shape of orbital in a division relationship)
                           m1,  // Orientation (2l + 1 orbitals)
                           mS,  // Orientation of electron's spin axis (one per electron)
                           averageRadius, // This will hold our (Low,Up) limits around 'value'

   };

The Quantum representation section helps simulate our quantity (in the example it’s 7). So the behavior of this type is based on probability (as quantum orbitals). This value doesn’t begin and end at 7, but exists spread around that number just like a nice butter spread :).

In terms of retrieving values, we can use the graph on the right of the following to probabilistically (depending on n, l,  m1, mS ) pick an unitary value for the QuantumOrb 7.

    QuantumOrb<int> x(7);
    cout << x << endl;    // 7
    cout << x << endl;    // 7.1
    cout << x << endl;    // 7.314

The type can be used to consistently output the same number using averageRadius although that would be strictly for backwards compatibility with the unitary paradigm.

Implications

Many that come to mind. Firstly in rendering, this is already seen in Voxels or volumetric pixels (that volume part can be represented with QuantumOrb type). See:

Secondly, stock market, where fluctuations always happen and predictions are harder to make. Interval types that keep track of orbital size changes (using averageRadius history) can maybe better focus the prediction problem on not a unitary value, but on an interval.

 

Thirdly, human quantification, namely people. We are never in one state, constantly fluctuating. From our health, emotions, decisions etc. it justifies adopting an interval based variable can more easily capture and predict our patterns in order to better social products (this would work great for the ad-space and marketers).

Takeaway

The main impression I want to leave you with is, we need to expand and stop thinking in absolutes with numbers. As a laymen example: If you ask me what time it is, it’s never right, because by the time I respond, it is a few million nanoseconds beyond whatever I am (will?) going to say. Hence adopting a more dualistic or “multi-listic” view and applying that to our most powerful tools and technologies will undeniably shift and better our understanding of reality and further our exploration!